Table of contents
- Q1. Height of trees
- Q2. InOrder Traversal
- Q3. PreOrder Traversal
- Q4. PostOrder Traversal
- Q5. LevelOrder Traversal
- Q6. Generate Tree from PreOrder and InOrder Traversal
- Q7. Generate Tree from PostOrder and InOrder Traversal
- Q8. Diameter of a tree
- Q9. Mirror of a given node
- Q10.Left/Right View
- Q11. Top/Bottom View
- Q12. Check for Balanced Binary Tree
- Q13. Vertical traversal
- Q14. Zigzag Traversal
- Q15.Diagonal Traversal of Binary Tree
- Q16. Boundary Traversal of binary tree
- Q17. Construct Binary Tree from String with bracket representation
- Q18. Construct string from binary tree
- Q19.Transform to Sum Tree
- Q20. Is sum tree?
- Q21.Binary Tree to DLL
- Q22. Flatten a Binary Tree to LL
- Q23.Minimum swap required to convert binary tree to binary search tree
- Q24.Check if Leaf are at same level
- Q25.Duplicate subtree in Binary Tree
- Q26.Check Mirror in N-ary tree
- Q27. Maximum path sum from any node
- Q28. Sum of nodes on the longest path from root to leaf node
- Q29. Maximum sum of Non-adjacent nodes
- Q30. Lowest Common Ancestor of a Binary Tree
- Q31. Min distance between two given nodes of a Binary Tree
- Q32.Kth Ancestor in a Tree
- Q33. Check if Tree is Isomorphic
Binary trees are fundamental data structures that offer a hierarchical organization of data, allowing for efficient search, insertion, and deletion operations.
In this blog post, we'll delve into some important questions related to binary trees, shedding light on their significance and functionality.
So, here we go!!!!!!!!!
Q1. Height of trees
int height(struct Node* node){
if(node){
int left= height(node->left);
int right = height(node->right);
return 1 + max(left,right);
}
return 0;
}
Q2. InOrder Traversal
//Recursive
vector<int> in;
vector<int> inOrder(Node* root) {
if(root!=NULL){
inOrder(root->left);
in.push_back(root->data);
inOrder(root->right);
}
return in ;
}
//Iterative
vector<int> ans;
vector<int> inOrder(Node* root)
{
stack<Node*> st;
while(root!=NULL || !st.empty()){
if(root!=NULL){
st.push(root);
root = root->left;
}
else{
root = st.top();
st.pop();
ans.push_back(root->data);
root=root->right;
}
}
return ans;
}
Q3. PreOrder Traversal
//recursive
void solve(Node *root,vector<int> &ans){
vector <int> preorder(Node* root)
{
vector<int> ans;
solve(root,ans);
return ans;
}
//iterative
vector<int> preOrder(Node* root)
{
vector<int> ans;
stack<Node*> st;
while(root!=NULL || !st.empty()){
if(root!=NULL){
ans.push_back(root->data);
st.push(root);
root=root->left;
}
else{
root = st.top();
st.pop();
root=root->right;
}
}
return ans;
}
Q4. PostOrder Traversal
//recursive
void solve(Node* root, vector<int> &post){
if(root){
solve(root->left,post);
solve(root->right,post);
post.push_back(root->data);
}
}
vector <int> postOrder(Node* root)
{
vector<int> post ;
solve(root,post);
return post;
}
//iterative
vector<int> postOrder(Node* node) {
// code here
vector<int> ans;
stack<Node*> st;
st.push(node);
if(node==NULL)return ans;
while(!st.empty()){
Node* temp = st.top();
st.pop();
ans.push_back(temp->data);
if(temp->left)st.push(temp->left);
if(temp->right)st.push(temp->right);
}
reverse(ans.begin(),ans.end());
return ans;
}
Q5. LevelOrder Traversal
vector<int> levelOrder(Node* node)
{
//Your code here
//queue
queue<Node*> q;
vector<int> ans;
q.push(node);
while(!q.empty()){
Node* t = q.front();
ans.push_back(t->data);
q.pop();
if(t->left)q.push(t->left);
if(t->right)q.push(t->right);
}
return ans;
}
//if return type is vector<vector<int>>, then one more while loop inside it, that counts on size of the queue, while(size--) and the same steps.
Q6. Generate Tree from PreOrder and InOrder Traversal
Example 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
int index = 0;
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
return generate(preorder,inorder,0,inorder.size()-1);
}
TreeNode* generate(vector<int>&preorder,vector<int>&inorder,int instart,int inend){
if(instart>inend)return NULL;
TreeNode* node = new TreeNode(preorder[index++]); //root
int splitindex = searchinInorder(inorder,instart,inend,node->val);
node->left = generate(preorder,inorder,instart,splitindex-1);
node->right = generate(preorder,inorder,splitindex+1,inend);
return node;
}
int searchinInorder(vector<int>& inorder,int instart, int inend, int val){
for(int i =instart;i<=inend;i++){
if(inorder[i]==val)return i;
}
return -1;
}
Q7. Generate Tree from PostOrder and InOrder Traversal
Example 1:

Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
Output: [3,9,20,null,null,15,7]
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int index = inorder.size()-1;
return generate(inorder, postorder, 0, inorder.size() - 1, index);
}
TreeNode* generate(vector<int>&inorder,vector<int>& postorder,int st, int end,int &index){
if(st>end || index<0)return NULL;
TreeNode* node = new TreeNode(postorder[index--]);
int split = search(inorder,st,end,node->val);
node->right = generate(inorder,postorder,split+1,end,index);
node->left = generate(inorder,postorder,st,split-1,index);
return node;
}
int search(vector<int>&inorder, int st, int end , int data){
for(int i =st;i<=end;i++)
if(inorder[i]==data)return i ;
return -1;
}
Q8. Diameter of a tree
Example 1:

Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].
int diameterOfBinaryTree(TreeNode* root) {
int ans = INT_MIN;
solve(root,ans);
return ans;
}
int solve(TreeNode*root,int &ans){
if(!root)return NULL;
int l = solve(root->left,ans);
int r = solve(root->right,ans);
ans = max(ans,l+r); //considering if the node is part of the solution then l+r
return 1+max(l,r); //if its not part of the solution then returning the max
}
Q9. Mirror of a given node
Example 1:
Input:
1
/ \
2 3
/ \ / \
4 5 6 7
and target = 4
Output: 7
Explanation: You can see below that the mirror
node of 4 is 7.
1 | 1
/ \ | / \
2 3 | 3 2
/ \ / \ | / \ / \
4 5 6 7 | 7 6 5 4
int res = -1;
int findMirror(Node *root, int target)
{
//code here
if(root->data==target)return root->data;
return solve(root->left,root->right,target);
}
int solve(Node* left,Node* right,int target){
if(!left||!right)return -1;
if(left->data==target) res = right->data;
if(right->data==target)res=left->data;
solve(left->left,right->right,target);
solve(left->right,right->left,target);
return res;
}
Q10.Left/Right View
1
/ \
2 3
/ \ / \
4 5 6 7
\
8
Left view of following tree is 1 2 4 8.
void solve(Node* root, int level, vector<int>&ans){
if(root==NULL)return ;
if(level == ans.size())ans.push_back(root->data);
solve(root->left,level+1,ans);
solve(root->right,level+1,ans);
}
vector<int> leftView(Node *root)
{
// Your code here
vector<int> ans;
solve(root,0,ans);
return ans;
}
Q11. Top/Bottom View
1
/ \
2 3
/ \ / \
4 5 6 7
Top view will be: 4 2 1 3 7
vector<int> topView(Node *root)
{
//Your code here
vector<int> ans;
if(root==NULL)return ans;
map<int,int> mp; //level, data
queue<pair<Node*, int>> q; //node, level
q.push({root,0});
while(!q.empty()){
auto it = q.front();
q.pop();
Node* node =it.first;
int line = it.second;
if(mp.find(line)==mp.end()){
mp[line] = node->data;
}
//for the bottom view, we will be updating the mp[line] everytime we encounter on the same line.
if(node->left!=NULL)q.push({node->left,line-1});
if(node->right!=NULL)q.push({node->right,line+1});
}
for(auto it: mp){
ans.push_back(it.second);
}
return ans;
}
Q12. Check for Balanced Binary Tree
Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: true
bool isBalanced(TreeNode* root) {
if(root==NULL)return 1;
bool ans=true;
solve(root,ans);
return ans;
}
int solve(TreeNode* root,bool &ans){
if(root==NULL|| ans==0)return 0;
int x = solve(root->left,ans);
int y = solve(root->right,ans);
if(abs(x-y)>1)ans= 0;
return 1+ max(x,y);
}
Q13. Vertical traversal
Example 1:
Input:
1
/ \
2 3
/ \ / \
4 5 6 7
\ \
8 9
Output:
4 2 1 5 6 3 8 7 9
Explanation:

vector<int> verticalOrder(Node *root)
{
//Your code here
vector<int> ans;
if(root==NULL)return ans;
map<int,vector<int>> mp ;
queue<pair<Node*,int>> q;
q.push({root,0});
while(!q.empty()){
auto it = q.front();
q.pop();
Node* node = it.first;
int level = it.second;
mp[level].push_back(node->data);
if(node->left) q.push({node->left,level-1});
if(node->right) q.push({node->right,level+1});
}
for(auto p : mp){
for(auto q:p.second){
ans.push_back(q);
}
}
return ans;
}
Q14. Zigzag Traversal
Example 1:
Input:
1
/ \
2 3
/ \ / \
4 5 6 7
Output:
1 3 2 4 5 6 7
vector <int> zigZagTraversal(Node* root)
{
// Code here
vector<int> ans;
if(root==NULL)return ans;
queue<Node*> q;
int level = 0;
q.push(root);
while(!q.empty()){
vector<int> temp;
int size = q.size();
while(size--){
auto it = q.front();
q.pop();
temp.push_back(it->data);
if(it->left)q.push(it->left);
if(it->right)q.push(it->right);
}
if(level%2!=0) reverse(temp.begin(),temp.end());
for(int i = 0 ; i<temp.size();i++)
ans.push_back(temp[i]);
level++;
}
return ans;
}
Q15.Diagonal Traversal of Binary Tree
Example 1:
Input :
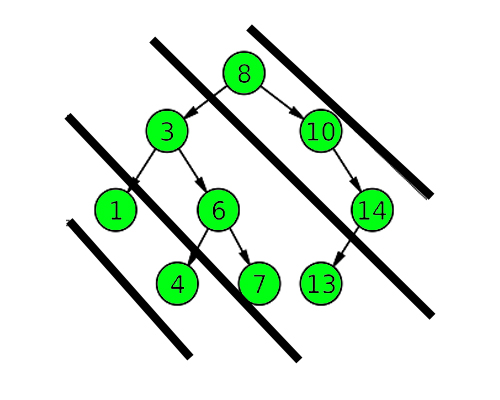
8
/ \
3 10
/ \ \
1 6 14
/ \ /
4 7 13
Output : 8 10 14 3 6 7 13 1 4
Explanation:
vector<int> diagonal(Node *root)
{
// your code here
vector<int> ans;
if(root==NULL)return ans;
queue<Node*> q;
q.push(root);
while(!q.empty()){
Node* node = q.front();
q.pop();
while(node){
if(node->left)q.push(node->left);
ans.push_back(node->data);
node = node->right;
}
}
return ans;
}
Q16. Boundary Traversal of binary tree
Input:
1
/ \
2 3
/ \ / \
4 5 6 7
/ \
8 9
Output: 1 2 4 8 9 6 7 3
Explanation:

void Leftnodes(Node* root, vector<int>&ans){
if(!root || (!root->left&&!root->right)) return ;
if(root->left){ // agr iska left hai matlab leaf nhi hai toh push kro aur isii pe chalo
ans.push_back(root->data);
Leftnodes(root->left,ans);
}
else if(root->right){
ans.push_back(root->data);
Leftnodes(root->right,ans);
}
}
void Leafnodes(Node* root, vector<int>&ans){
if(!root) return ;
Leafnodes(root->left,ans);
if(!root->left&& !root->right) ans.push_back(root->data);
Leafnodes(root->right,ans);
}
void Rightnodes(Node* root,vector<int>&ans){
if(!root || (!root->left&&!root->right)) return ;
if(root->right){
Rightnodes(root->right,ans);
ans.push_back(root->data);
}
else if(root->left){
Rightnodes(root->left,ans);
ans.push_back(root->data);
}
}
vector <int> boundary(Node *root)
{
//Your code here
vector<int> ans ;
if(!root)return ans;
ans.push_back(root->data);
Leftnodes(root->left,ans);
if (root->left || root->right) {
Leafnodes(root,ans);
}
Rightnodes(root->right,ans);
return ans;
}
Q17. Construct Binary Tree from String with bracket representation
Input: "4(2(3)(1))(6(5))"
Output: 3 2 1 4 5 6
Explanation:
4
/ \
2 6
/ \ /
3 1 5
Node *treeFromString(string str){
// code here
Node* root= new Node(0);
solve(root,str);
return root;
}
int i =0;
void solve(Node* root, string str){
if(i<str.size()&& isdigit(str[i])){
int sum =0;
while(i<str.size()&& isdigit(str[i])){
sum = sum *10;
sum = sum + str[i]-'0';
i++;
}
root->data = sum ;
}
if(i<str.size()&& str[i]=='('){
i++;
if(i<str.size()&& str[i]==')') i++;
else{
root->left =new Node(0);
solve(root->left, str);
}
}
if(i<str.size()&& str[i]=='('){
i++;
if(i<str.size() && str[i]==')')i++;
else{
root->right =new Node(0);
solve(root->right, str);
}
}
if(i>=str.size() || str[i]==')'){
i++;
return ;
}
}
Q18. Construct string from binary tree
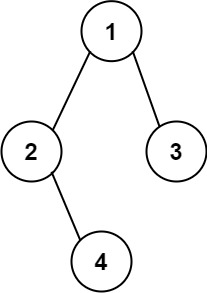
Input: root = [1,2,3,null,4]
Output: "1(2()(4))(3)"
string tree2str(TreeNode* root) {
string ans="";
solve(root,ans);
return ans;
}
void solve(TreeNode* root, string &ans){
if(root==NULL)return;
ans+=to_string(root->val);
if(root->left){
ans+="(";
solve(root->left,ans);
ans+=")";
}
if(root->right){
if(!root->left)ans+="()";
ans+="(";
solve(root->right,ans);
ans+=")";
}
}
Q19.Transform to Sum Tree
Input:
10
/ \
-2 6
/ \ / \
8 -4 7 5
Output:
20
/ \
4 12
/ \ / \
0 0 0 0
void toSumTree(Node *node)
{
// Your code here
solve(node);
return;
}
int solve(Node* node){
if(node==NULL)return 0;
int val = node->data;
node->data = solve(node->left) + solve(node->right);
return val + node->data;
}
Q20. Is sum tree?
Input:
3
/ \
1 2
Output: 1
bool isSumTree(Node* root)
{
// Your code here
bool ans = true ;
solve(root,ans);
return ans;
}
int solve(Node* root, bool &ans){
if(root==NULL || ans==false)return 0;
int l = solve(root->left,ans);
int r = solve(root->right,ans);
if(!root->left&&!root->right)return root->data;
if(root->data != l + r)ans = false;
return root->data + l + r;
}
Q21.Binary Tree to DLL
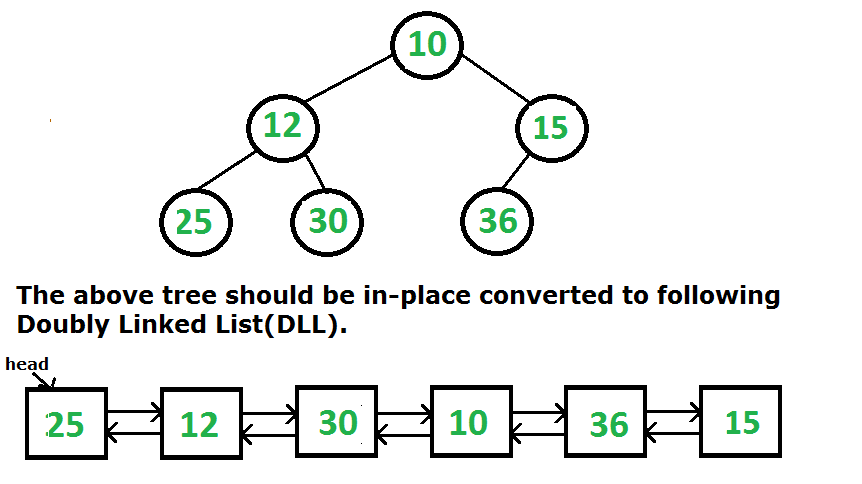
Node * bToDLL(Node *root)
{
// your code here
Node* head = NULL;
Node* prev = NULL;
int h = 0 ;
solve(root,head,prev,h);
return head;
}
void solve(Node* root, Node* &head,Node* &prev, int &h ){
if(root==NULL)return ;
solve(root->left,head,prev,h);
if(h==0){
//means its the first node ie head;
h=1;
head = root;
prev = root;
}
else{
prev->right = root;
prev->right->left = prev;
prev = prev->right; //or prev=root;
}
solve(root->right, head, prev, h );
}
Q22. Flatten a Binary Tree to LL
Input :
1
/ \
2 5
/ \ \
3 4 6
Output :
1 2 3 4 5 6
Explanation:
After flattening, the tree looks
like this
1
\
2
\
3
\
4
\
5
\
6
TreeNode* prev = NULL;
void flatten(TreeNode* root) {
if(root==NULL)return ;
flatten(root->right);
flatten(root->left);
root->right = prev;
root->left = NULL;
prev = root;
}
Q23.Minimum swap required to convert binary tree to binary search tree
Example 1:
Input:
A[] = { 5, 6, 7, 8, 9, 10, 11 }
Output: 3
Explanation:
Binary tree of the given array:

Swap 1: Swap node 8 with node 5.
Swap 2: Swap node 9 with node 10.
Swap 3: Swap node 10 with node 7.
So, minimum 3 swaps are required.
vector <int> in;
void inorder(vector<int> &A,int index){
if(index>=A.size()) return;
inorder(A,2*index+1);
in.push_back(A[index]);
inorder(A,2*index+2);
}
int minSwaps(vector<int>&A, int n){
//Write your code here
inorder(A,0);
vector<pair<int,int>> v;
for(int i=0;i<n;i++)v.push_back({in[i],i});
sort(v.begin(),v.end());
int count = 0;
for(int i=0;i<n;i++){
if(i==v[i].second)continue;
else{
swap(v[i],v[v[i].second]);
count++;
i--;
}
}
return count;
}
Q24.Check if Leaf are at same level
Input: 10 / \ 20 30 / \ 10 15 Output: 0
int ans;
bool check(Node *root)
{
//Your code here
int k = -1;
int h = 1;
ans = 1;
solve(root,h,k);
return ans;
}
void solve(Node* root,int h,int&k){
if(!root)return ;
if(ans==0)return ;
if(!root->left && !root->right){ //leaf node found
if(k==-1) k = h; //first leaf node
else{
if(k!=h) ans = 0;
}
return;
}
solve(root->left,h+1,k);
solve(root->right,h+1,k);
}
Q25.Duplicate subtree in Binary Tree
1
/ \
2 3
/ \ \
4 5 2
/ \
4 5
Output : 1
//2 critical cases :
//1st when there's no track between the sides of children, so we need a separator
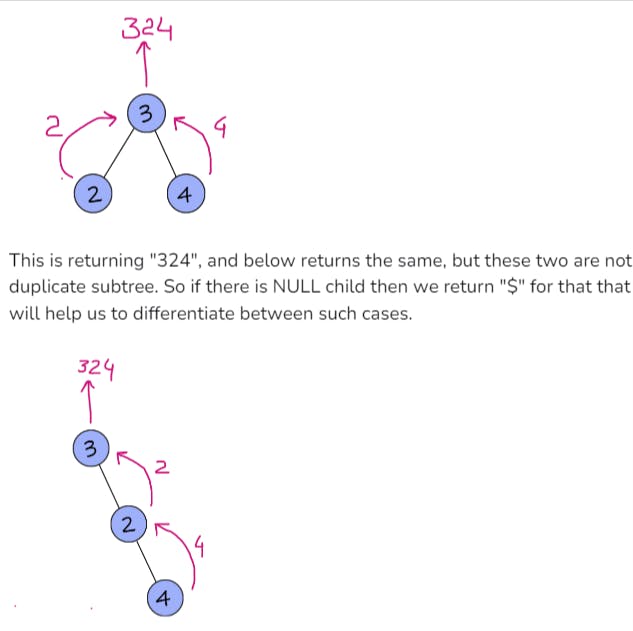
//2nd in case of different vals of nodes but same results, therefore separator is needed
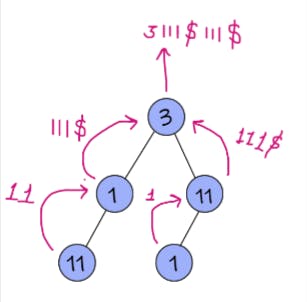
unordered_map<string,int> mp;
int dupSub(Node *root) {
// code here
solve(root);
for(auto i : mp)if(i.second>=2)return 1;
return 0;
}
string solve(Node* root){
string s = "";
if(!root)return "$";
if(!root->left && !root->right){
s = s+to_string(root->data);
return s;
}
s= s+to_string(root->data);
s+='/';
s= s+solve(root->left);
s+='/';
s= s+solve(root->right);
mp[s]++;
return s;
}
Q26.Check Mirror in N-ary tree
n = 3, e = 2
A[] = {1, 2, 1, 3}
B[] = {1, 3, 1, 2}
Output:
1
Explanation:
1 1
/ \ / \
2 3 3 2
int checkMirrorTree(int n, int e, int A[], int B[]) {
// code here
unordered_map<int,stack<int>> mp ;
for(int i =0;i<2*e;i+=2){
mp[A[i]].push(A[i+1]);
}
for(int i = 0 ; i<2*e;i+=2){
if(mp[B[i]].top() != B[i+1])return 0 ;
mp[B[i]].pop();
}
return 1;
}
Q27. Maximum path sum from any node
10
/ \
2 -25
/ \ / \
20 1 3 4
Output: 32
Explanation: Path in the given tree goes
like 10 , 2 , 20 which gives the max
sum as 32.
int maxi = INT_MIN;
int findMaxSum(Node* root)
{
// Your code goes here
solve(root);
return maxi;
}
int solve(Node* root){
if(!root)return 0;
int leftsum = max(0,solve(root->left));
int rightsum = max(0,solve(root->right));
maxi = max(maxi, root->data + leftsum + rightsum);
return root->data + max(leftsum, rightsum);
}
Q28. Sum of nodes on the longest path from root to leaf node
Input: 4 / \ 2 5 / \ / \ 7 1 2 3 / 6
Output: 13
int ans = INT_MIN;
int maxlevel = 0;
int sumOfLongRootToLeafPath(Node *root)
{
solve(root,1,0);
return ans;
}
int solve(Node* root,int level, int sum){
if(!root)return 0;
sum+=root->data;
if(level>maxlevel){
maxlevel = level ;
ans = sum;
}
else if(level==maxlevel){
ans = max(ans,sum);
}
solve(root->left,level+1,sum );
solve(root->right,level+1,sum);
}
Q29. Maximum sum of Non-adjacent nodes
Input:
1
/ \
2 3
/ / \
4 5 6
Output: 16
Explanation: The maximum sum is sum of
nodes 1 4 5 6 , i.e 16.
unordered_map<Node*,int> m;
int getMaxSum(Node *root)
{
// Add your code here
return solve(root);
}
int solve(Node* root){
if(!root)return 0;
if(m[root]) return m[root];
//with root
int withroot = root->data;
if(root->left){
withroot+=solve(root->left->left);
withroot+=solve(root->left->right);
}
if(root->right){
withroot+=solve(root->right->right);
withroot+=solve(root->right->left);
}
//without root
int withoutroot = solve(root->left) + solve(root->right);
return m[root] = max(withroot,withoutroot);
}
Q30. Lowest Common Ancestor of a Binary Tree

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==NULL) return NULL;
if(root==p || root==q)return root;
TreeNode* left = lowestCommonAncestor(root->left,p,q);
TreeNode* right = lowestCommonAncestor(root->right,p,q);
if(left==NULL)return right;
else if(right==NULL)return left;
else return root; //both are not null
}
Q31. Min distance between two given nodes of a Binary Tree
Input: 1 / \ 2 3
a = 2,
b = 3
Output: 2
//approach :
// first find their LCA
// then find distance of both the nodes from their LCA
int findDist(Node* root, int a, int b) {
Node* LCA = lca(root,a,b);
//distance of both the nodes from our lca
int x = distance(LCA,a);
int y = distance(LCA,b);
return x+y-2;
}
Node* lca(Node*root,int a,int b){
if(root==NULL)return NULL;
if(root->data==a||root->data==b)return root;
Node* l = lca(root->left,a,b);
Node* r = lca(root->right,a,b);
if(l==NULL)return r;
else if(r==NULL)return l ;
else return root;
}
int distance(Node* root,int n){
if(root==NULL)return 0;
if(root->data == n)return 1;
int goleft = distance(root->left,n);
int goright = distance(root->right,n);
if(!goleft && !goright)return 0;
else return 1 + goleft + goright;
}
Q32.Kth Ancestor in a Tree
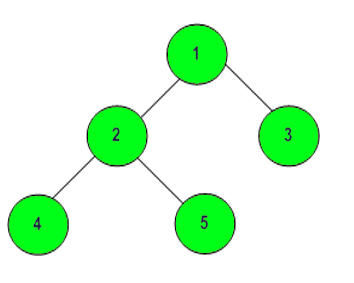
K = 2 Node = 4
Output: 1
//by backtracking
int kthAncestor(Node *root, int k, int node)
{
int cnt = k ;
int val =-1;
solve(root,cnt,node,val);
return val;
}
int solve(Node* root, int &cnt, int &node, int&val){
if(!root)return 0;
if(root->data==node)return 1;
int l = solve(root->left,cnt,node,val);
int r = solve(root->right,cnt,node,val);
if(l || r) {
//ie we got 1 from either l or r so decrease the count
//if the cnt is 0 means reached
cnt--;
if(cnt==0)val = root->data;
return 1;
}
return 0;
}
Q33. Check if Tree is Isomorphic
Tree obtained from another tree after a series of swaps are known to be isomorphic
Input: T1 1 T2: 1 / \ / \ 2 3 3 2 / / 4 4
Output: No
Input: T1 1 T2: 1 / \ / \ 2 3 3 2 / \ 4 4
Output: Yes
//tree can be obtained from another tree by a series of swaps- isomorphic trees
bool isIsomorphic(Node *root1,Node *root2)
{
//add code here.
if(!root1 && !root2)return 1;
if(!root1 || !root2) return 0;
if(root1->data !=root2->data)return 0;
//case 1: they are swapped already, so just checking
bool a = isIsomorphic(root1->left,root2->right)
&& isIsomorphic(root1->right,root2->left);
//case2: they aren't swapped, but can become identical by swapping
bool b = isIsomorphic(root1->left,root2->left)
&& isIsomorphic(root1->right,root2->right);
return a || b;
}